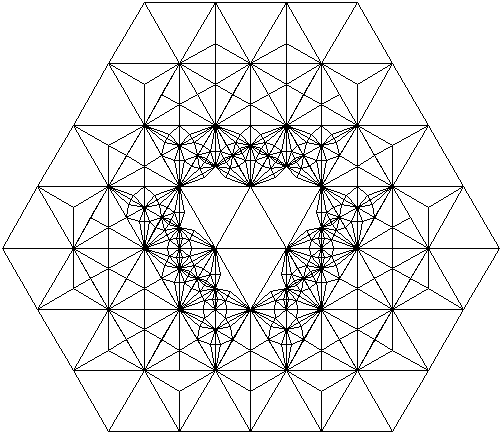This group of tetrahedrons starts with the group for the mu lepton. All paths of two steps or less from the last two steps of the mu lepton group and all but six of the three step paths that come from two directions are included. This produces 447 different tetrahedrons. The matrices in this shape are as follows. The list includes only one permutation of the first three numbers.
| (1) |
(21) |
(121) (321) (421) |
(3121) (4121) (1321) (2321) (4321) (1421) (3421) |
(13121) (43121) (14121) (34121) (21321) (41321) (12321) (42321) (14321) (24321) (34321) (21421) (31421) (13421) (23421) |
(213121) (413121) (143121) (343121) (214121) (314121) (134121) (121321) (321321) (421321) (141321) (241321) (341321) (412321) (142321) (242321) (214321) (314321) (124321) (324321) (134321) (234321) (121421) (321421) (421421) (131421) (231421) (431421) (213421) (413421) (123421) (323421) (423421) |
(1213121) (3213121) (4213121) (1413121) (2413121) (3413121) (1214121) (3214121) (4214121) (1314121) (2314121) (4314121) (1412321) (1214321) (1314321) (2324321) (4134321) (4234321) (2321421) (1213421) |
(24213121) (23214121) |
The sum of all the matrices used to generate this shape is
| 527 497 497 471 0 |
497 527 497 471 0 |
497 497 527 471 0 |
2522 2522 2522 2529 0 |
-3596 -3596 -3596 -3495 447 |
The sum of columns is (1992 1992 1992 10095 -16071)
The sum of products is 3*3968064+3*20109240 = 72231912
The volume ratio is sqrt(72231912/6) = 3469.676
The mass ratio of a tau lepton to an electron is 3477.6
A projection of this shape onto a plane follows.

A projection of this shape from the other side follows.